Week 3: Random Dungeons
This Week's Music, and some Bonus Music because I can't resist.
This week we will
- Learn about The Pseudo-random Number God, and adapt a simple and effective one into Haskell ourselves.
- Learn about the
RandomGenandRandomtypeclasses. - Learn about the
MonadRandomtypeclass and theSTtype. - Write a Random Dungeon Generator.
There was a little mix up last week where I was saying "it should all compile now" but I'd forgotten to talk about some part of some small change I'd made so it didn't actually compile for people following along. Usually I code ahead a bit and then write things down once I've had some success, so it can be hard to remember every single little change, particularly as we start having more than one file.
Starting this week, when I pause at a concept and mention that we want to check for a successful compile and run I'll include a link to a specific commit of that point. If you run into trouble you can check against that commit. Of course, there will still be the link to a commit at the end of the week's work as well.
(Pseudo-)Random Number Generators
There's lots of pseudo-random number generators (PRNGs) in the world. They have all sorts of techniques that you might use. I'm not an expert but we can talk about it a bit anyway because at the basic level it's quite simple. You might be used to the phrase "random number generator", and I keep sticking "pseudo-" on the front, so what's that mean? It means that our random number generator isn't actually random in the sense of "entirely unpredictable". That's very hard to do, and pretty much has hardware requirements (usually by measuring the timing of something external to the computer, like user input frequencies, radioactive decays of an isotope sample, cloud movements, or something else like that). If you take the chaotic data (called entropy) from a hardware source like that and hook it up to a randomization technique you can get a "truly random number generator" (probably, true randomness might not exist in our universe, but some people hope for its existence). Even then your hardware has to be really good for your inputs to be statistically random. The other trouble is that even when you do it all just right, it's slooooooow. The speed of your random number generation is limited by how fast you get more entropy, and that's far too slow for most purposes.
How do we go faster? That's where the "pseudo-" comes in. A pseudo-random number generator is the sort of thing where you say to yourself, "as long as me and my friends (or enemies) can't predict the next value from just looking at the other values so far, that's probably good enough, right?" And, indeed, it pretty much is good enough. A pseudo-random number generator takes some initial data, some initial amount of bits, which is called the seed. Our seed might come from some sort of entropy source, it might come from a number that the user typed in for us to use, we might just get lazy and use the system clock, something like that. Then some sort of math is done to make a random-seeming number and the next seed. If we wanted put it in Haskell terms we'd say something like this:
runTheGenerator :: SeedValue -> (Output,SeedValue)
What's so cool about this compared to the "truly random" generators? Well, since our generator gives us a random output and also a new seed to use, we can run it again on our new seed without needing to go get more entropy. We can keep running it over and over as fast as our processor can go to make as many random numbers as we want. It's so sweet that people who aren't being technical don't even use the "pseudo-" part when talking about pseudo-random number generators, they just assume that you're always using a pseudo-random number generator, and use "random number generator" (RNG) for short.
That's the short version. Here's a whole presentation about the subject if you've got the hour. It's a great talk, and you should watch it. She covers a bit of the history of RNG techniques, and how you can decide what's a good RNG and what's a bad RNG, and so forth. I'll wait while you watch, don't worry.
Done? Good. So Haskell has a package called random which provides the basic interface for pure random number geneators via a typeclass, along with a generator that they call StdGen. We'll be using their typeclass, but I happen to know from personal experience that if we use a PCG based RNG on a 64-bit machine we can go 2-3 times faster than StdGen in the same amount of space used. I've got benchmarks to prove it and everything. Since pretty much everyone has 64-bit machines these days we'll use a PCG based generator.
Let's look at the "minimal" C version that the professor from the presentation provides on her pcg website
// *Really* minimal PCG32 code / (c) 2014 M.E. O'Neill / pcg-random.org
// Licensed under Apache License 2.0 (NO WARRANTY, etc. see website)
typedef struct { uint64_t state; uint64_t inc; } pcg32_random_t;
uint32_t pcg32_random_r(pcg32_random_t* rng)
{
uint64_t oldstate = rng->state;
// Advance internal state
rng->state = oldstate * 6364136223846793005ULL + (rng->inc|1);
// Calculate output function (XSH RR), uses old state for max ILP
uint32_t xorshifted = ((oldstate >> 18u) ^ oldstate) >> 27u;
uint32_t rot = oldstate >> 59u;
return (xorshifted >> rot) | (xorshifted << ((-rot) & 31));
}
Alright, well, first of all this is under the Apache 2.0 license. That's not a copyleft license, so our project doesn't have to also be Apache 2.0 just by using this, but it does remind me that my repo defaulted to the MIT license, and I should fix that. This whole tutorial project is Public Domain, use it as you like. That change will show up in the repo with this week's release.
So we have a struct. How do we do C structs in Haskell? With the data keyword. We'll call our generator PCGen instead of PCG32RandomT because it's a lot shorter, and ending types with T has a special convention associated with it in Haskell that we'll get to in a bit.
data PCGen = PCGen Word64 Word64 deriving (Read, Show)
This is a different looking way of using the data keyword for us. This is just like the record syntax version in terms of the way memory is used and such, but the fields don't have names, so we don't get any accessors auto-generated for us, and we can't use the record update syntax. That's fine, since we will never want to use one part of the generator without the other anyway.
We're importing Data.Word because the default imports of Haskell only include the Word type, which is for unsigned values of whatever width your machine uses (32-bit or 64-bit). It switches around on different machines because usually you don't care about the exact limit, and it's generally faster to use numbers with the same width as your hardware's machine width whenever possible. With our type we need to ensure that we're specifically using Word64 values so that they will overflow properly when we do the multiplication stuff. On a 64-bit machine Word and Word64 are identical, but on a 32-bit machine it will fall back to emulating 64-bit values at the software level. Somewhat slower, but I'll take correct and slow over wrong and fast any day.
So the C code has a function procedure that takes a pointer to a generator and gives an output. The generator gets mucked with during the process. We could write this exact code in Haskell if we wanted,
pcg32randomr :: Ptr PCGen -> IO Word32
That's a little gross though. You lose your old generator since you're overwriting the Ptr data, and since you're using IO to do it GHC can't collapse intermediate steps and inline and redorder things as much as it normally might, so all that optimization work falls on your shoulders instead. I don't wanna do all that. Let's try a better way.
stepGen :: PCGen -> (Word32,PCGen)
Hey look, it's totally coincidentally just like the runTheGenerator function I proposed above. Neat. So we build up a bunch of intermediate values with bit shifting and give back an output and the next generator. Those sorts of operations are in Data.Bits, so we'll import that too.
stepGen :: PCGen -> (Word32,PCGen)
stepGen (PCGen state inc) = let
newState = state * 6364136223846793005 + (inc .|. 1)
xorShifted = fromIntegral (((state `shiftR` 18) `xor` state) `shiftR` 27) :: Word32
rot = fromIntegral (state `shiftR` 59) :: Word32
out = (xorShifted `shiftR` (fromIntegral rot)) .|. (xorShifted `shiftL` fromIntegral ((-rot) .&. 31))
in (out, PCGen newState inc)
We're making four temporary bindings, then giving our output. We do have to carefully control what numeric types are used at each stage or the math will come out wrong, so that's what the extra :: Word32 parts are doing with the fromIntegral stuff.
fromIntegral :: (Num b, Integral a) => a -> b
It lets us convert types like Int and Word into any other numeric type. Let's break it down:
stateandincare bothWord64of course.newStateis alsoWord64.statetimes 6364136223846793005 is aWord64,incOR'd with 1 is aWord64, and then adding them together we still haveWord64. Haskell will make number literals be whatever type they need to be. If the number literal is bigger than the type it's being used with you'll get a warning too (eg5000 :: Word8would give a warning, sinceWord8only goes from 0 to 255).xorShiftedwould normally beWord64, because it'sstateshifted right 18 bits, then XOR'd with the start value, then that shifted down 27 bits, which leaves us with aWord64at the end. However, we usefromIntegralat the very end and we specify that we want our target type to beWord32. This keeps just the lowest 32 bits.rotis the same deal. We shift ourstatevalue down by 59 bits and cast it intoWord32, giving us a 5-bit value (0 to 31).outis where we fiddle thexorShiftedvalue around based on the bits inrot, so that's allWord32math.
If you're wondering why we're doing any of this nonsense, you sure didn't watch the presentation, now did you?
Great, so now we can do random numbers!
Standard Crypto Disclaimer: If you're actually doing cryptographic work you should prefer a tried and true RNG technique that has been shown to be of a cryptographic grade, and you should probably use an implementation that has been heavily tested as well instead of rolling your own. We're not using such a generator because it's only a video game so "much faster" beats out "provably secure".
RandomGen and Random
Now that we can make random numbers, we'll talk about some stuff from the random package.
RandomGen
The random package provides a typeclass called RandomGen for types which can be used as a random source, which has three methods.
next :: RandomGen g => g -> (Int, g)
genRange :: RandomGen g => g -> (Int, Int)
split :: RandomGen g => g -> (g, g)
If we want our PCGen type to work nicely with other randomization stuff in the Haskell ecosystem, we have to give it a RandomGen instance. To do that, we use the instance keyword and then define an implementation for each method in the typeclass. For reasons I'm not quite sure of, you actually can't provide type signatures on instance definitions by default. You can turn on the InstanceSigs extension if you really want, but it's not a big deal so we'll leave the type sigs off this time.
instance RandomGen PCGen where
next gen = let
(outWord, nextGen) = stepGen gen
outInt = fromIntegral (fromIntegral outWord :: Int32) :: Int
in (outInt, nextGen)
Alright, so we're saying that to get an Int out of our generator, you run the generator with stepGen, giving you a new generator and a Word32. Then, to get that Word32 into an Int properly, you turn it into an Int32 first (which causes the highest bit to become a sign bit) and then convert that into an Int. If we converted straight to Int from Word32 we'd end up with always positive output on 64-bit machines and output that's split positive and negative on 32-bit machines. I don't expect that we'll run on 32-bit machines, but if that's where we end up it'll be weird, so let's avoid that possibility. GHC's optimization pass will make short work of simple numeric type changing code either way.
genRange _ = (fromIntegral (minBound :: Int32), fromIntegral (maxBound :: Int32))
This is a function that lets users know what the lower and upper bounds of the results of this generator are. In our case, the entire range of Int32 is a potential output, but again we must cast it to Int.
split gen@(PCGen state inc) = let
(q,nGen1@(PCGen sa ia)) = stepGen gen
(w,nGen2@(PCGen sb ib)) = stepGen nGen1
(e,nGen3@(PCGen sc ic)) = stepGen nGen2
(r,nGen4@(PCGen sd id)) = stepGen nGen3
stateA = sd `rotateR` 5
stateB = sd `rotateR` 3
incA = ((fromIntegral q) `shiftL` 32) .|. (fromIntegral w)
incB = ((fromIntegral e) `shiftL` 32) .|. (fromIntegral r)
outA = PCGen stateA (incA .|. 1)
outB = PCGen stateB (incB .|. 1)
in (outA, outB)
One method that you might not expect to see is called split, which uses the generator to make two "unrelated" generators, so that you can break up your random streams as you do recursive descents or whatever else you want like that. This just does some nonsense math to produce generators that are disconnected by making some totally new seed and inc values.
Those patterns with the @ makes it so that you can pattern match and unpack a value while also having a name for the whole value.
Random
There's also a Random typeclass for types that you can produce values of using a RandomGen. It has two methods that are required:
randomR :: (RandomGen g, Random a) => (a, a) -> g -> (a, g)
random :: (RandomGen g, Random a) => g -> (a, g)
We can make PCGen have a Random instance too.
instance Random PCGen where
random gen = let
(x,newGen) = random gen
in (PCGen x x,newGen)
randomR _ gen = random gen
So random takes a RandomGen, uses next to produce a Word64, then uses that as both fields in the PCGen it returns. randomR is supposed to be for producing values within a (lower,upper) range, but with our generator it's pretty much nonsense to say that there's one generator "between" two other generators, so we just do exactly what random does and ignore the tuple entirely.
Random Dungeon Generation
With that all out of the way we're ready to get to work. I'll be using the pcgen package, which has a version of PCGen type with a little extra fanciness beyond what we've covered here. Same basic interface though.
We import Data.PCGen and System.Random, then add a field for the PCGen in our GameState type, and update mkGameState as well.
data GameState = GameState {
gameGen :: PCGen,
playerPos :: (Int,Int),
dungeon :: Dungeon
} deriving (Read, Show)
mkGameState :: PCGen -> Int -> Int -> GameState
mkGameState gen xMax yMax = GameState gen (5,5) (mkDungeon xMax yMax)
And adjust how we start the game in main
startingGen <- randomIO
gameRef <- newIORef $ mkGameState startingGen cols rows
randomIO uses the global random number generator to produce a Random value. In this case, it's producing a PCGen for us. We use the global RNG to get started, but after that we'll only be relying on our own generator for randomness. While we're at it, we'll rename mkDungeon to boxDungeon since we're about to have more than one way to make Dungeon values. And since the Dungeon type is starting to develop, we'll move it into its own module/file so that the Main module doesn't get too cluttered. Haskell lets you have as much as you want in a module, it's just our own human limits that make us want to keep things organized. Each module has its own file, so we start a Dungeon.hs file and move some stuff over: Terrain, Dungeon, boxDungeon, and getTerrainAt.
Which reminds me that our drawing code doesn't use getTerrainAt, and it's also a little wonky, so let's clean it up and switch over to doing things more properly in the process. Just after the tileID, BG, and FG colors we'll change it to this:
(px,py) = playerPos gameState
d = dungeon gameState
cellCount = rows*cols
updateList = map (\cellIndex -> let
(r,c) = cellIndex `divMod` cols
x = c
y = rows - (r+1)
in if px == x && py == y
then (playerID, playerBG, playerFG)
else case getTerrainAt (x,y) d of
Open -> (openID, openBG, openFG)
Wall -> (wallID, wallBG, wallFG)
_ -> (1, playerBG, playerFG)) [0 .. cellCount -1]
You might be able to spot where I'm leaving the space for later shifting to having a "viewport" area that we can scroll so that the dungeon size doesn't have to be the exact same size as our window. We'll get to that in a bit.
Monad Transformers
Yikes! this is where things get weird. Because we're going to be using some stuff called Monad Transformers, but to explain that you should really have read like four chapters worth of material out of some sort of book that let you work up to the concept, and then spend another entire chapter on the actual concept itself. Nobody has time for actual learning, so I'm going to explain it gloss it all over in one long paragraph.
- There are things with a typeclass called
Functor, which are a particular sort of abstract structure(ish). If you take aFunctortype and compose it with anotherFunctortype, the resulting type is still aFunctor. Example:Maybe aand[a]are both Functors, so[Maybe a]is also a Functor. - Some
Functortypes are also anApplicative, which means that their abstract structure(ish) nature follows particular additional rules which we don't need to go into at the moment. Like withFunctor, when you compose two differentApplicativetypes you always get a result type that's stillApplicative. - Some
Applicativetypes are also aMonad, which means that their abstract structure(ish) nature follows yet more particular rules that we won't go into at the moment. This is the break in the pattern: an arbitraryMonadtype composed with another arbitraryMonadtype is not still aMonad. There's math and proofs to back this sad truth up, and you can try to do it for yourself, but it turns out that if you want to compose twoMonadtypes you need to know what at least one of them is or you can't do it. - Sometimes we really want to compose our monads though. Some situations are just begging for a little bit of composed monad to be the answer. So we have a group of types called Monad Transformers. By convention, a monad transformer is named after the normal
Monadthat it duplicates the behavior of, with a T at the end.MaybeandMaybeTStateandStateTReaderandReaderTEitherandExceptT(whoops we broke the pattern)RandandRandT- You get the idea
- You take your "base" monad and then stack some transformer types on top, and then you can write functions that intermix all sorts of monadic things. Not every
Monadtype offers a transformer variant. Things likeIO,ST, andSTMalways need to be the base of your monad stack if they are in the stack. - The order that you stack things affects how the whole combination actually works. However, individual functions that just rely on a particular
FooMonadcapability being present somewhere in the stack don't usually care what the exact order is. To handle this we have typeclasses that let functions accessMonadfunctionality regardless of where that is in the current stack of monads.MonadIOlets you do IO as long asIOis the base of yourMonadstack (remember that it must always be the base if it's present).MonadRandomlets you do RNG stuff as long as there's an RNG somewhere.MonadReaderlets you read context variables as long as they're somewhere.- Again, you get the idea.
Okay. Now, I know that's a lot, but unfortunately for the next function I show you to make sense we need to do one more side bit.
The ST type
Sometimes in Haskell we want to "mutate" a value and it's fine that technically we're making an entirely new value with a little bit changed and then throwing away the old value. It's a few bytes here and there, the garbage collector can handle it. A small price to pay for easy concurrency and easy reasoning about the program.
Sometimes it's not fine. Sometimes you've got a Vector of 80*24=1920 values, and you want to change just one of them at a time, but you don't want to allocate an entirely new Vector for every single change, because you plan on making dozens and dozens of changes before you're through, and that's way too much garbage. So we want to be able to perform destructive, in-place updates.
Well, you can use a mutable variant of Vector. Except... the write function has a constraint of "PrimMonad m". Clicking that, we come to a page where the docs say, "Class of monads which can perform primitive state-transformer actions". The list of known instances says IO, ST s, and a bunch of things built from transformers.
All of our internal logic is free of IO so far, and it'd be a shame to change that. If our dungeon generation is IO, then anything that even might geneate a dungeon needs to be IO, so that includes all player movement, and so that basically includes the whole game. Ugh. Let's check out that ST stuff that it links to.
"The strict state-transformer monad." yada yada yada... woah.
runST :: (forall s. ST s a) -> a
That's new, we've never seen a forall in a type signature before. Better back up and actually read what they were saying.
"A computation of type ST s a transforms an internal state indexed by s, and returns a value of type a. The s parameter is either
- an uninstantiated type variable (inside invocations of
runST), or RealWorld(inside invocations ofstToIO).
It serves to keep the internal states of different invocations of runST separate from each other and from invocations of stToIO."
Hmm. And the documentation on runST says a little more
"Return the value computed by a state transformer computation. The forall ensures that the internal state used by the ST computation is inaccessible to the rest of the program."
Okay, so what they're saying is that when you use id :: a -> a you can pick the type that a becomes for that use of id, and when you use runST :: (forall s. ST s a) -> a you can't pick the type of the s. The code you write has to be polymorphic to all possible s values, so you effectively can't touch s yourself. The Haskell runtime will do that for you. All you can do is affect the a portion. So you build up an ST s a expression, then use runST on it and the ST portion of it all gets extracted away during the computation, leaving you with just the a at the end. Neat.
How does this connect to mutable vectors again? Well, it turns out that we can have those destructive, in-place updates that we want, as long as we only do them with values tagged with that wondrous s. This includes mutable vectors when our PrimMonad m requirement is satisfied with ST s. To the outside world, it's exactly as if we hadn't used destructive updates at all. Things tagged with the s can't escape the runST, so we have to "freeze" our mutable vector back into an immutable one at the end. Note that saying "they can't escape" is not just a friendly suggestion, you get a special kind of type error if you try:
RL-tut> import Control.Monad.ST
RL-tut> import Data.STRef
RL-tut> runST (newSTRef True)
<interactive>:4:8: error:
* Couldn't match type `a' with `STRef s Bool'
because type variable `s' would escape its scope
This (rigid, skolem) type variable is bound by
a type expected by the context:
ST s a
at <interactive>:4:1-21
Expected type: ST s a
Actual type: ST s (STRef s Bool)
* In the first argument of `runST', namely `(newSTRef True)'
In the expression: runST (newSTRef True)
In an equation for `it': it = runST (newSTRef True)
* Relevant bindings include it :: a (bound at <interactive>:4:1)
As long as we don't try to drag the s outside our ST context things work just like IO and IORef
RL-tut> runST $ do { r <- newSTRef True; writeSTRef r False; readSTRef r }
False
In fact, ST is exactly like a limited form of IO that you can tear away when you're done with it. So we'll make a mutable vector within ST, perform all of our changes to make a random dungeon, and then "freeze" the result into an immutable vector at the end of the ST computation.
Actually a Dungeon, finally.
Okay, so we use replicate from Data.Vector.Mutable (imported as VM), we use getRandomR from the MonadRandom typeclass, and it looks like we're ready to go:
rogueDungeon :: RandomGen g => Int -> Int -> g -> (Dungeon,g)
rogueDungeon width height g = let
(tileVector, gFinal) = runST $ flip runRandT g $ do
let count = width*height
vec <- VM.replicate count Open
x1 <- getRandomR (1,20)
x2 <- getRandomR (1,20)
y1 <- getRandomR (1,20)
y2 <- getRandomR (1,20)
setBox width vec (x1,y1) (x2,y2) Wall
V.unsafeFreeze vec
in (Dungeon width height tileVector, gFinal)
Neat.
What just happened?
Okay... so the type signature says that we're taking two Int values, and a RandGen g, and we get a (Dungeon,g) tuple back. That's a lot like the next method, we just have a few extra values at the start. I think that makes sense so far.
So we use runST on... a flipped runRandT with the generator which is used on... a do block.
flip :: (a -> b -> c) -> b -> a -> c
-- easier to make sense of if you put an extra set of parentheses in
-- same type though, the -> brackets to the left.
flip :: (a -> b -> c) -> (b -> a -> c)
runRandT :: RandT g m a -> g -> m (a, g)
flip runRandT :: g -> RandT g m a -> m (a, g)
So flip just takes a function and swaps around the order that it accepts arguments in:
runRandT is RandT -> Generator -> BaseMonadAction
flipped is Generator -> RandT -> BaseMonadAction
Using flip on runRandT prevents us from having to have the whole do block in parentheses and then a tiny little g at the end.
In this case, the base monad action is an ST s (Vector Terrain, RandomGen g), which runST unwraps into just (Vector Terrain, RandomGen g). That kinda makes sense I guess.
Honestly this transformer stuff can be hard to wrap your head around. I stared at all the types and docs involved for several minutes before I just started to experiment a bit and got it after a few tries. That part at the outside where you have to chain a bunch of runFoo uses together just right is the worst. I always forget and have to stop and think very carefully when I get to a new transformer stack in a new project. If this doesn't make sense to you, don't worry, it barely makes sense to me too. Just have faith that GHC will not hesitate to call you out when your types don't line up. Ask others for help if you need to.
Inside the do block, we're making a new (mutable) Vector of the correct size with Open terrain in all the positions. Then we pick four random numbers that are each from 1 to 20, use setBox (we'll get to that in a moment), and then freeze the mutable vector into being a mutable one. Alright, not so bad I guess. Since we won't mutate the vector after we freeze it, it's safe to use unsafeFreeze and avoid a copy. Since it's the last line of the do block, the result of that expression becomes the result of the do block without us having to use pure. That's actually all pure does anyway, is form an action that immediately gives back the same value you pass to it so that the value can be the result of the do block as a whole.
What is setBox? Well, it just sets the rectangle you specify to be the value you specify. It's trying to simulate a 2d grid but vectors are only 1d, so setBox needs to know the "width" of the grid rows so that it can turn 2d coordinates into 1d indexes. Sounds easy? It is easy! The type signature is not so fun to look at though :/
setBox :: PrimMonad m => Int -> VM.MVector (PrimState m) a -> (Int,Int) -> (Int,Int) -> a -> m ()
setBox width vec (x1,y1) (x2,y2) tile = do
let xmin = min x1 x2
xmax = max x1 x2
ymin = min y1 y2
ymax = max y1 y2
targets = do
y <- [ymin .. ymax]
x <- [xmin .. xmax]
pure $ width*y+x
mapM_ (\i -> VM.write vec i tile) targets
Ouch, yeah. Ugly type signature. You can split them over more than one line if you want when they get like this. Same rules apply as with normal expressions: lines after the first have to be indented some amount more than the first line.
-- We can do it one argument per line or mix and match how we like
-- With two arguments per line it looks like this.
setBox :: PrimMonad m =>
Int -> VM.MVector (PrimState m) a ->
(Int,Int) -> (Int,Int) ->
a -> m ()
The vector writing code itself is kinda what you expect if you've worked with "2d" vectors/arrays before. This is our first use of a list via its Monad instance though. Unlike with IO, ST, and RandT, with List the <- doesn't just compute one value and bind it to a variable, it computes every value and then runs everything below it once for each possible value. So y runs through every value from ymin to ymax, and for each step of that x runs from xmin to xmax, and for each step of that we produce a single index value. Then we use mapM_ to write to each index value with the new tile value. mapM is like map, but for when the function you're mapping is monadic. The version with the underscore at the end means to throw away the results immediately because we don't care. There are slightly different typeclass constraints between the two, but they both would work here, so we'll pick the version that explicitly discards the result because it makes our intent more clear.
We'll use this with mkGameState
-- | Constructs a GameState with the player at 5,5
mkGameState :: PCGen -> Int -> Int -> GameState
mkGameState gen xMax yMax = let
(d,g) = rogueDungeon xMax yMax gen
in GameState g (5,5) d
and now you get a random blob of wall that changes every time you start the program: commit.
Actually A Useful Dungeon
So the generator we'll be doing works like this:
- We start the whole map with wall tiles
- We divide the map into a 3 by 3 grid conceptually. If the map doesn't divide evenly, outer edges might have a tile or two of overflow.
- Into each grid sector we carve one room that's randomly sized within that sector's bounds. We also keep track of the room sizes for the next steps.
- Between the sectors there are 12 border regions. Each of the little line segments of a
#. So we go through the numbers 1 through 12 and connect the rooms of each border region. If we wanted to have less than full corridor saturation we could try to track what rooms are connected or not yet, connect in a random order, and then stop once everything is connected, but I don't feel like it. I like more twisty passages than less. - The room connection process is that we pick a point that's open within each room and draw a line connecting them. If the two points selected don't align in the direction we're drawing (which is likely), then we'll have to pick a midpoint between the rooms and draw the hallway from each side to that midpoint, and then have the hallways turn toward each other at the midpoint.
Easy enough to understand I think. That's about how Rogue does it, and I'm told that's also about how Angband does it. They have target minimums on room sizes, which we don't. I'm not sure if that'll be an issue or not until we see some results.
Speaking of seeing results, we should change gameUpdate so that is has a key to let us re-run the dungeon generator. Then we can cycle dungeons without having to shut down and restart out program over and over. We just add a new case to out existing case.
Key'R -> \gameState -> let
gen = gameGen gameState
xMax = dungeonWidth $ dungeon gameState
yMax = dungeonHeight $ dungeon gameState
in mkGameState gen xMax yMax
This might well be some fiddly geometry nonsense, so don't be afraid to use the Debug.Trace module to check things as they're evaluated if you really need to. It's about as clumsy as any other "println debugging" in other languages, but it works when your expressions are too big for easy ghci testing. As the module says, "These can be useful for investigating bugs or performance problems. They should not be used in production code."
First we move our ability to pick a random sector into its own space.
randSector :: (MonadRandom m) => Int -> Int -> Int -> Int -> m (Int,Int,Int,Int)
randSector xlow xhigh ylow yhigh = do
x1 <- getRandomR (xlow,xhigh)
x2 <- getRandomR (xlow,xhigh)
y1 <- getRandomR (ylow,yhigh)
y2 <- getRandomR (ylow,yhigh)
pure $ (x1,y1,x2,y2)
Now that we're actually putting it in a type signature instead of just using one of its methods, we have to add MonadRandom from Control.Monad.Random.Class to our imports. ghci is effectively one giant IO block, and IO has a MonadRandom instance, so we can run this in ghci without any special ceremony if we need to.
RL-tut> randSector 0 23 0 79
(7,34,9,8)
RL-tut> randSector 0 23 0 79
(12,63,1,41)
RL-tut> randSector 0 23 0 79
(20,59,4,73)
Here's the crap part. Now we have to use that thing. Each sector's bounding box is essentially unique to it, and since we don't want the rooms to actually touch each other, we have to throw in some offsets too. Maybe I'm missing out on some sort of super math, but this is what I came up with:
rogueDungeon :: RandomGen g => Int -> Int -> g -> (Dungeon,g)
rogueDungeon width height g = let
tileCount = width*height
secWidth = width `div` 3
secHeight = height `div` 3
(tileVector, gFinal) = runST $ flip runRandT g $ do
vec <- VM.replicate tileCount Wall
-- decide our sector locations
sectors <- forM [1..9] $ \i -> do
let (xlow,xhigh,ylow,yhigh) = case i of
1 -> (1, secWidth-1, 1, secHeight-1)
2 -> (secWidth+1, 2*secWidth-1, 1, secHeight-1)
3 -> (2*secWidth+1, width-2, 1, secHeight-1)
4 -> (1, secWidth-1, secHeight+1, 2*secHeight-1)
5 -> (secWidth+1, 2*secWidth-1, secHeight+1, 2*secHeight-1)
6 -> (2*secWidth+1, width-2, secHeight+1, 2*secHeight-1)
7 -> (1, secWidth-1, 2*secHeight+1, height-2)
8 -> (secWidth+1, 2*secWidth-1, 2*secHeight+1, height-2)
9 -> (2*secWidth+1, width-2, 2*secHeight+1, height-2)
randSector xlow xhigh ylow yhigh
-- draw the sectors
forM_ sectors $ \(x1,y1,x2,y2) ->
setBox width vec (x1,y1) (x2,y2) Open
-- TODO: connect the sectors
V.unsafeFreeze vec
in (Dungeon width height tileVector, gFinal)
Woop woop. forM and forM_ are flipped versions of mapM and mapM_ respectively. They're from Control.Monad. Ah, but we left ourselves a bit of a TODO there.
-- do all of the connections
forM_ [1..12] $ \borderIndex -> do
let (sec1targ, sec2targ, isVert) = case borderIndex of
1 -> (1,2,False)
2 -> (2,3,False)
3 -> (4,5,False)
4 -> (5,6,Flase)
5 -> (7,8,False)
6 -> (8,9,False)
7 -> (1,4,True)
8 -> (4,7,True)
9 -> (2,5,True)
10 -> (5,8,True)
11 -> (3,6,True)
12 -> (6,9,True)
sec1 = sectors !! (sec1Targ-1)
sec2 = sectors !! (sec2Targ-1)
-- if rooms aren't lined up we might have to draw more than one hall
-- to connect two rooms, so we get them back as a list and then map
-- over that list.
halls <- pickHallway sec1 sec2 isVert
forM_ halls $ \(x1,y1,x2,y2) ->
setBox width vec (x1,y1) (x2,y2) Open
Alright, another ugly giant switch. And we're calling some sort of pickHallways deal,
-- | Given two room bounds, and a hint about if they're vertically oriented with
-- each other or not, we return the list of hallways that should be drawn to
-- connect the rooms.
pickHallways :: MonadRandom m => (Int,Int,Int,Int) -> (Int,Int,Int,Int) -> Bool -> m [(Int,Int,Int,Int)]
pickHallways (s1x1,s1y1,s1x2,s1y2) (s2x1,s2y1,s2x2,s2y2) isVert = if isVert
then do -- the sectors are over top each other (we're looking for X)
-- TODO
pure []
else do -- the sectors are side by side (we're looking for Y)
let s1ymin = min s1y1 s1y2
s1ymax = max s1y1 s1y2
s2ymin = min s2y1 s2y2
s2ymax = max s2y1 s2y2
yRange = S.toAscList $ S.intersection
(S.fromAscList [s1ymin..s1ymax])
(S.fromAscList [s2ymin..s2ymax])
if null yRange
then -- we need a turn
else do -- we don't need a turn
y <- getRandomR (head yRange,last yRange)
pure [(s1x1,y,s2x1,y)]
Ugh this is a mess! We're not even done filling out pickHallways and it's already too hard to know what's going on. Do you know what went wrong? We didn't let the data types do any of the work for us. Let's back up and do this a little more properly. Here's the cliff notes:
-- We keep this.
rogueDungeon :: RandomGen g => Int -> Int -> g -> (Dungeon,g)
-- We're going to have a proper type for Room values
randRoom :: (MonadRandom m) => Int -> Int -> Int -> Int -> m Room
-- same as before, but using mkRoom now
-- the '!' makes the values here strict by default
data Room = Room !Int !Int !Int !Int
deriving (Show)
mkRoom :: (Int,Int) -> (Int,Int) -> Room
mkRoom (x1,y1) (x2,y2) = let
xlow = min x1 x2
ylow = min y1 y2
xhigh = max x1 x2
yhigh = max y1 y2
in Room xlow ylow xhigh yhigh
drawRoom :: PrimMonad m => Int -> VM.MVector (PrimState m) Terrain -> Room -> m ()
-- uses setBox
data Orientation = Vertical | Horizontal deriving Show
type Hall = Room -- Note: we might make these more distinct later
drawHall :: PrimMonad m => Int -> VM.MVector (PrimState m) Terrain -> Hall -> m ()
-- uses setBox
Now we need a way to tell when two rooms are overlapping in either X or Y. Since we can't be sure that either of our two room values are the "lesser" value, it's a little annoying to do this ourselves. However, we can imagine that each room as a set of valid coordinates in the direction we care about, and then let some sort of Set datatype in some library figure it for us. Turns out that there is such a library.
{- New Imports -}
-- containers
import Data.Set (Set)
import qualified Data.Set as S
{- new functions -}
overlapX :: Room -> Room -> Set Int
overlapX (Room r1xl _ r1xh _) (Room r2xl _ r2xh _) =
S.intersection
(S.fromAscList [r1xl .. r1xh])
(S.fromAscList [r2xl .. r2xh])
overlapY :: Room -> Room -> Set Int
overlapY (Room _ r1yl _ r1yh) (Room _ r2yl _ r2yh) =
S.intersection
(S.fromAscList [r1yl .. r1yh])
(S.fromAscList [r2yl .. r2yh])
Okay phew. When your type signatures get shorter, it's a sign that you've probably broken the process up into smaller chunks that are easier to think about at once. Now we just need to make some random hallways.
-- | Given two room bounds, and a hint about if they're vertically oriented with
-- each other or not, we return the list of hallways that should be drawn to
-- connect the rooms.
pickHallways :: MonadRandom m => Room -> Room -> Orientation -> m [Hall]
pickHallways r1@(Room r1xl r1yl r1xh r1yh) r2@(Room r2xl r2yl r2xh r2yh) Vertical = do
mayX <- uniformMay (overlapX r1 r2)
case mayX of
Just x -> pure [mkRoom (x,min r1yl r2yl) (x,max r1yh r2yh)]
Nothing -> do
-- there's no overlap, we need to make a turn-hallway
pure [] -- FIXME
pickHallways r1@(Room r1xl r1yl r1xh r1yh) r2@(Room r2xl r2yl r2xh r2yh) Horizontal = do
mayY <- uniformMay (overlapY r1 r2)
case mayY of
Just y -> pure [mkRoom (min r1xl r2xl,y) (max r1xh r2xh,y)]
Nothing -> do
-- there's no overlap, we need to make a turn-hallway
pure [] -- FIXME
uniformMay is another MonadRandom utility. We give it something implementing Foldable, and it'll pick a value out of that randomly. Checking the Set type, it seems that a Set is Foldable. Lucky us. Except that we get the value back as a Maybe, because the Foldable might be empty, and there'd no way to pick a value if there's no values to pick from. That's fine for us, because we already needed to know about that situation. So we pick randomly from the overlap, and if we get a selection we can make a single hallway from that. If we didn't get a selection there was no overlap and we'll have to make two partial hallways with a turn. This is a little tricky, so for now we'll just do nothing at all and give back an empty list of no hallways in that case. Let's run our program we have to so far and see if it covers the simple case properly.
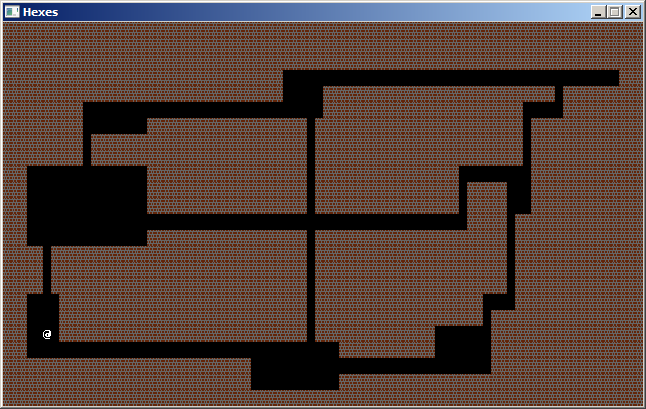
Oh cool, it does work! commit
Some Cleanup
The first bit of cleanup is that we want to limit how much we're exporting from the Dungeon module. Similar to imports, we use parens to limit what Dungeon exports. This way all the dungeon generation internals won't be given out to the world. Partly because we don't want people trying to use our tools for all the intermediate steps, and partly because when GHC sees that something is private to our module it will let itself be even more aggressive about optimizations.
module Dungeon (
Terrain(..),
Dungeon(..),
boxDungeon,
rogueDungeon,
getTerrainAt
) where
And at the top of our file we can use {-# LANGUAGE Trustworthy #-}, which marks the module as not doing anything crazy. The "Safe Haskell" system tries to improve confidence in code by splitting modules into three general levels.
- Safe is when you're not even allowed to import any unsafe functionality.
- Trustworthy is when you're allowed to import unsafe things but you're making a claim to the outside world that your API is safe to use despite using unsafe features internally.
- Unsafe is when your module deliberately exposes an unsafe API and your users need to pay attention when they're playing with your stuff.
Vector and the primitive stuff can't be imported safely, so our module can't be Safe. Instead, we mark it as Trustworthy to assure people that we paid attention while writing things and we're at least not deliberately letting them shoot themselves in the foot. Bugs might show up, but that's life.
Now, the rooms can be generated in a slightly cleaner way, but not much cleaner since we ultimately do need to have one line for each sector. Any more compact and you get really hard to read code. About the best we can do is something like this.
rooms <- sequence [
randRoom 1 (secWidth-1) 1 (secHeight-1),
randRoom (secWidth+1) (2*secWidth-1) 1 (secHeight-1),
randRoom (2*secWidth+1) (width-2) 1 (secHeight-1),
randRoom 1 (secWidth-1) (secHeight+1) (2*secHeight-1),
randRoom (secWidth+1) (2*secWidth-1) (secHeight+1) (2*secHeight-1),
randRoom (2*secWidth+1) (width-2) (secHeight+1) (2*secHeight-1),
randRoom 1 (secWidth-1) (2*secHeight+1) (height-2),
randRoom (secWidth+1) (2*secWidth-1) (2*secHeight+1) (height-2),
randRoom (2*secWidth+1) (width-2) (2*secHeight+1) (height-2)
]
sequence is a new one.
sequence :: (Monad m, Traversable t) => t (m a) -> m (t a)
So the list of actions is transformed into a single action that gives back the whole list at once. Neat.
We can cut down some of the hallway stuff, but we're mostly still stuck with a big ugly thing. Oh well. We can read it, which is what's important, even if it's not the most graceful possible thing. Sometimes code is just good enough and you should move on with your life. commit